油壓缸能力計算

作用力

對單桿式油缸而言，當液壓油進入腔側建立壓力後，圓形的受壓面積會產生最大的(推)作用力，而另一側的桿側受壓面是圓環形，因此產生的(拉)作用力會小於腔側的(推)作用力。 根據使用方式，雙桿式油缸產生的作用力可以是推力，也可以是拉力。 需注意的是，由於雙桿式油缸兩側的受壓面都是圓弧形，這代表它的推力會小於相同缸徑與桿徑的單桿式油缸。

\[ 作用力-腔側入油 \\[12pt] F = {1 \over 4} {\pi P D^2} \\[24pt] 作用力-桿側入油 \\[12pt] F = {1 \over 4} {\pi P (D^2-d^2)} \\[24pt] \small{ \begin{align*} F &= \{ \, N \, \} \\[4pt] D &= \{ \, mm \, \} \\[4pt] d &= \{ \, mm \, \} \\[4pt] P &= \{ \, MPa \, \} \end{align*} } \]

移動速度

油缸的基本運動為靜止 → 加速 → 等速 → 減速 → 靜止，移動速度是指等速運動階段的速度，同時也是最快的速度，與入油流量與受壓面積有關，在相同流量下，桿側入油時的桿速會快於腔側。

\[ 移動速度-腔側入油 \\[12pt] V = {{4 \, Q} \over {\pi \, D^2}} \\[24pt] 移動速度-桿側入油 \\[12pt] V = {{4 \, Q} \over {\pi \, (D^2-d^2)}} \\[24pt] \small{ \begin{align*} V &= \{ \, mm/s \, \} \\[4pt] D &= \{ \, mm \, \} \\[4pt] d &= \{ \, mm \, \} \\[4pt] Q &= \{ \, mm^3/s \, \} \end{align*} } \]

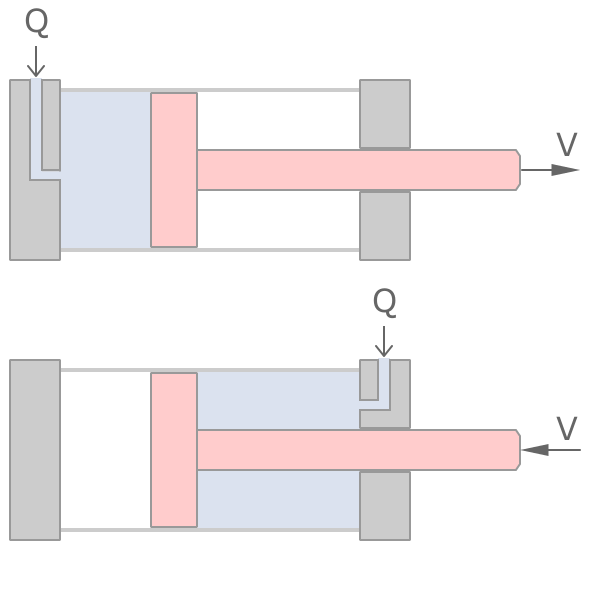
行程費時

行程費時指的是等速運動過程所花費的時間，與移動速度有關，而加、減速階段所花費的時間通常在整個行程中佔比小，因此忽略。 在相同流量下，桿側入油的行程完成時間會短於腔側。

\[ 行程費時-腔側入油 \\[12pt] t = {{\pi \, S} \over {4 \, Q}} \, D^2 \\[24pt] 行程費時-桿側入油 \\[12pt] t = {{\pi \, S} \over {4 \, Q}} \, (D^2-d^2) \\[24pt] \small{ \begin{align*} t &= \{ \, s \, \} \\[4pt] D &= \{ \, mm \, \} \\[4pt] d &= \{ \, mm \, \} \\[4pt] Q &= \{ \, mm^3/s \, \} \end{align*} } \]

吐出流量

往復運動的油壓缸，桿側或腔側至少有一側會經歷入油與出油的過程，如單動式油缸的一側入油，會使另一側的彈簧受到壓縮，直到入油側的壓力被釋放，回復的彈簧將會反向推動活塞，迫使原先的入油側向外排油，轉為出油側，這時排出的流量稱為吐出流量； 雙動式油缸的入、出油側交替，一般是透過油壓迴路中的電磁閥來控制。

\[ 吐出流量-腔側入油 \\[12pt] q = {(D^2-d^2) \over D^2} \, Q \\[24pt] 吐出流量-桿側入油 \\[12pt] q = {D^2 \over (D^2-d^2)} \, Q \\[24pt] \small{ \begin{align*} q &= \{ \, mm^3/s \, \} \\[4pt] D &= \{ \, mm \, \} \\[4pt] d &= \{ \, mm \, \} \\[4pt] Q &= \{ \, mm^3/s \, \} \end{align*} } \]

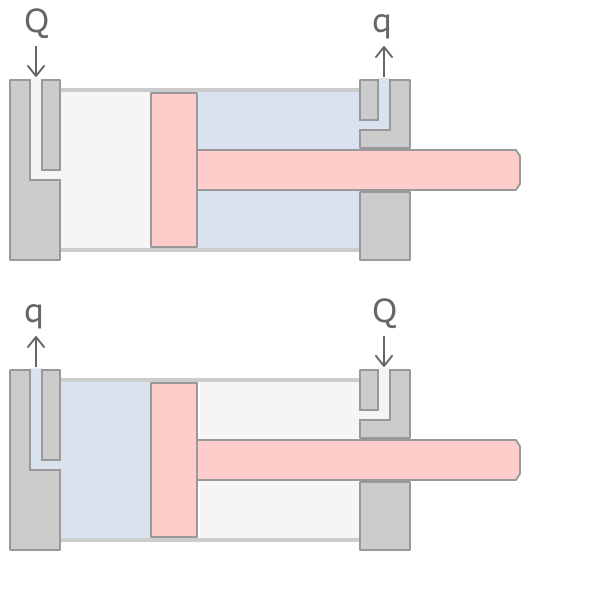
消耗功率

油壓缸要在設定的壓力與流量下運作，需要消耗一定的能量。 泵浦馬達的額定功率在扣除馬達效率損失、泵浦效率損失、管路損失後，必會大於消耗功率，也就是說可以藉由消耗功率來推算泵浦的馬達大小。 這裡的計算結果只適合應用在油壓缸，不可用於氣壓缸。

推拉比

單桿式油缸有著不同的推力與拉力，因此常使用推拉比來表示二力大小的差距，同時也是桿側入油的與腔側入油的桿速比。